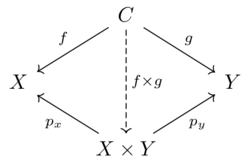
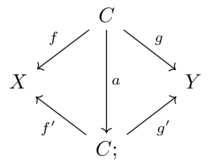
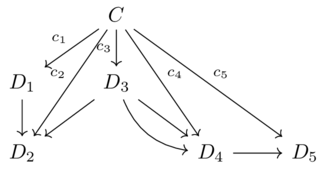
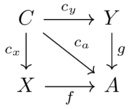
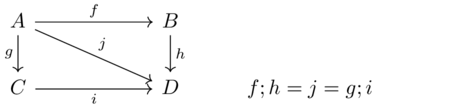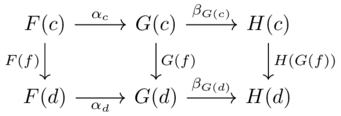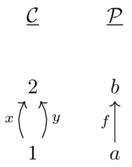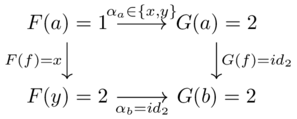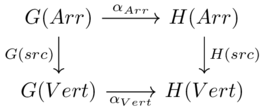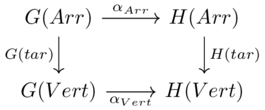What is a database(3)
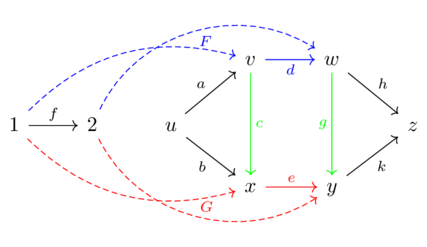
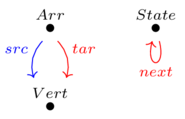
A database is a system of interlocking tables.
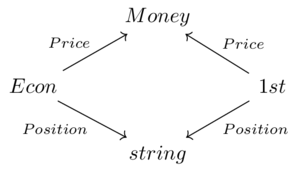
Some columns are internal references (i.e. foreign keys), others are external references (string, int, etc.).
Changing the internal reference value doesn’t mean anything (if we do it consistently), but not for the external references.
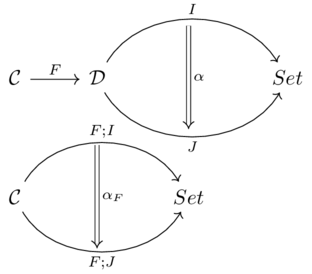
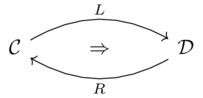
Category theory provides a mathmetical approach for translating between two different database representations of a common domain.
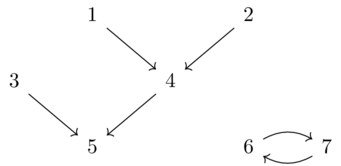
Exercise 3-3(2)
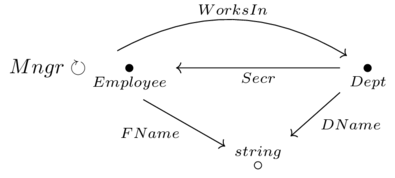
Count the number of non-ID columns in the following database and compare to the number of foreign keys in the database schema.
| Employee | FName | WorksIn | Mngr |
|---|---|---|---|
| 1 | Alan | 101 | 2 |
| 2 | Ruth | 101 | 2 |
| 3 | Kris | 102 | 3 |
| Dept | DName | Secr |
|---|---|---|
| 101 | Sales | 1 |
| 102 | IT | 3 |
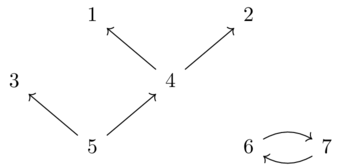
Solution(1)
They are the same: 5